摘要:在非理想流场条件下,异径dn150供水计量表传感器将产生较大的测量误差。提高传感器权函数分布均匀度,有助于提高传感器的非理想流场测量性能。因此,需要开展传感器权函数分布规律的研究。基于有限元软件COMSOL,分析了4种异径dn150供水计量表传感器权函数的均匀度,结果表明:矩形异径传感器的权函数*均匀。建立矩形异径dn150供水计量表传感器三维模型,研究权函数与矩形段长宽高的分布规律,结果表明:矩形段高度对权函数均匀性的影响*大,宽度稍小,长度影响*小。矩形段的高度和宽度越小,权函数分布越均匀,测量结果受非理想流场的影响越小。
引言
异径dn150供水计量表传感器由于安装空间狭小、前后没有理想直管段,管道内被测流场通常是非理想流场,将导致测量值与真实值存在较大偏差、影响计量精度。为提高非理想流场的测量性能,需要研究合适的异径截面形状和尺寸,以提高传感器内权函数分布的均匀度。然而国内外相关的研究较少。ShercliffJA和BevirMK等人*次提出和深化了dn150供水计量表的权函数理论。卫开夏等人利用ANSYS有限元软件求解非满管dn150供水计量表的权函数分布。孔令富等人使用MATLAB软件中的PDE工具箱对权函数进行有限元求解。王月明等人基于ANSYS对含有非导电物质时的dn150供水计量表进行有限元分析。李雪菁采用COMSOLMultiphysics有限元软件求解非绝缘管dn150供水计量表的权函数分布。王经卓等人基于COMSOL软件,利用流体像素的方法求解dn150供水计量表权函数的分布。上述文献主要针对圆管dn150供水计量表传感器点电*的二维权函数进行分析,其研究结果与实际三维情况存在偏差。同时,尚未有人针对异径dn150供水计量表传感器三维权函数的分布规律进行研究。由于无可参考的非理想流场测量工况的理论依据,研发人员无法确定究竟何种异径截面有助于提高权函数均匀度,也无法确定哪一种尺寸有助于提高权函数均匀度。针对这一问题,本文从理论上研究权函数与耦合电动势关系,确定提高权函数分布均匀度有助于非理想流场测量。通过COMSOL软件采用电场模拟法,分析4种不同异径截面dn150供水计量表传感器的权函数分布均匀度,确定较优的异径截面形状。针对优选异径截面形状的圆电*dn150供水计量表传感器,研究权函数分布均匀度与异径段长宽高之间的规律。所得结论为异径dn150供水计量表传感器的测量管结构尺寸设计提供了一定的参考,也为提高异径dn150供水计量表传感器的非理想流场测量性能提供了理论依据。
1、dn150供水计量表传感器检测原理
当导电性液体在磁场中作切割磁力线运动时,液体中有感应电流产生。假定液体的电导率δ是均匀、各向同性的,则欧姆定律的普遍公式写作
式中j→为电流密度矢量,为通过液体单位面积的电流,A/m2;E→为电场强度矢量,V/m;v→为流体速度,m/s;B→为磁感应强度,T。当激励电流角频率ω不大时,流体中的位移电流完全可以忽略,即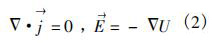
将式(2)带入式(1)得dn150供水计量表传感器的基本测量方程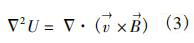
式中U为感应电动势,V;2为拉普拉斯算子;为哈密顿算子。
通常借助Green函数G来求解微分方程(3),G满足Laplace方程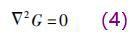
根据传感器的管道形状和电绝缘边界条件,建立了完整形式的dn150供水计量表传感器基本方程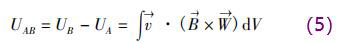
式中V为dn150供水计量表传感器测量空间;W→为权函数。在直角坐标系(x,y,z)中,式(5)可以转换为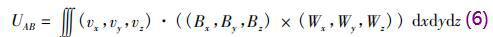
若磁感应强度在传感器有效工作区间内分布均匀,则磁感应强度B=By,Bx=Bz=0,式(6)可以化为
当流速为轴向流时,即v=-vz,vx=vy=0;则式(7)表示为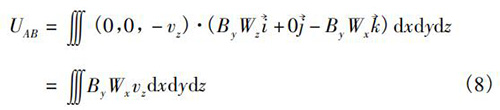
同时,若传感器内的权函数分布均匀,Wx=W,则式(8)变为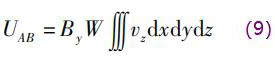
传感器内的权函数分布均匀时,感应电动势大小只与流速积分值成正比,不依赖于流型的分布,有利于非理想流场的精确测量。
2权函数仿真与分析
dn150供水计量表传感器内的流体微元切割磁力线产生感应的电势和电位,相当于一个个微小的“电源”。某一点的权函数应为该点微元作为“电源”所产生的电位梯度与电*间电位差之比。所以,可以采用电场模拟法测定权函数:传感器空间内充满导电液体(一般为水),在电*处施加一定的电压,便会在导电介质中形成一个电场,测得各点的电场强度,并除以中心点的电场强度,即得到归一化后的权函数值,将其绘制成等值线图便可得到权函数分布图。
2.1仿真方法
基于电场模拟法,选择COMSOLMultiphysics有限元仿真软件求解权函数步骤如下:
1)使用AC/DC模块中的电流应用程序模式,圆管半径为32mm,点电*半径0.4mm,仿真模型为二维模型;
2)电*材质设置为金属铜,导电液体为水,电导率为1×10-4S/m;
3)测量管具有绝缘衬里,满足电绝缘边界条件n→×j→=0,左右电*分别施加1,-1V的电压;
4)划分四边形网格,为了保证仿真结果的精确度,选择*细化网格;
5)使用稳态求解器进行计算,得到各点处的电场强度,并除以中心点处的电场强度,得到归一化后的权函数值。
2.2结果分析
2.2.1不同异径面的影响
为考察不同异径截面权函数分布的均匀性,使用上述方法对圆形、正方形、八边形和矩形异径截面的权函数分布进行定性分析。为了便于对比,设置管道口径为DN100,异径部分截面积为3200mm2。所以,圆形异径面半径为32mm,正方形异径面边长为56.6mm,八边形异径面边长为25.8mm,矩形异径面长宽为80×40mm。仿真结果如图1所示,为了便于对比,权函数等势线大小从0开始,以0.25为步长递增到30。由图1(a)~图1(d)可知,矩形异径截面的权函数等势线间距*大,即权函数变化梯度*小,权函数分布*均匀。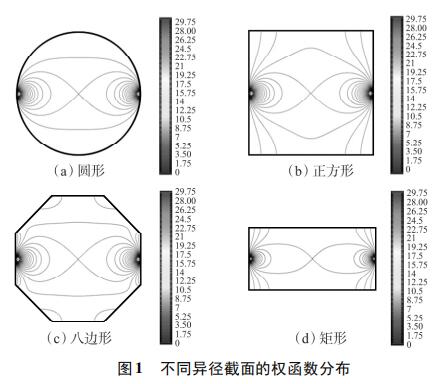
为了客观评价不同异径截面内权函数分布的均匀程度,采用整体均匀度来定量衡量权函数的均匀性,设电*截面内每个节点的权函数值为 Wk,相应截面的权函数平均值为 W0,则电*截面内权函数的整体均匀度 R 为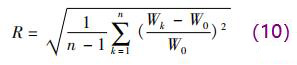
通过式( 10) 计算得到圆形、正方形、八边形、矩形 4 种
不同异径截面权函数分布的整体均匀度分别为 1. 811 2, 1. 996 9,1. 915 0,1. 563 9。
综上所述,矩形异径结构的权函数分布*均匀,所以,异径dn150供水计量表传感器采用矩形异径的管道结构,该结构权函数分布比较均匀,能够减少非理想流场引入的测量误差。在实际生产实践过程中,权函数分布与矩形段长 L、宽 D、 高 H 有关,因此,开展了矩形异径圆电*dn150供水计量表传感器的三维权函数建模分析,*终得到一种权函数分布比较均匀的结构尺寸。
2. 2. 2 三维权函数分布
使用 Pro /E 软件建立三维几何模型,导入 COMSOL 软件进行有限元求解。仿真模型如图 2 所示,电*连线为x 轴,连线中点为坐标原点,流体运动方向为 z 轴,传感器管道口径为 DN100,总长250 mm。异径管部分初始结构尺寸 L = 80 mm,D = 80 mm,H = 40 mm,圆形电*半径为17 mm,伸出绝缘衬里的*大距离为 1. 5 mm。
1) 长度的影响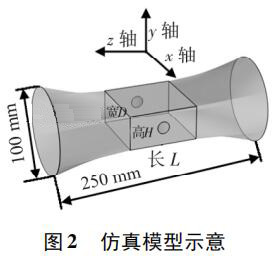
*先分析一定 D × H 条件下,L 变化时传感器内的权函数分布情况。由于传感器异径管部分高度 H 越小信号越强,但压损也越大,因此,H 设置为 30 ~ 50 mm; 异径管宽度 D 越大压损越小,但宽度越大传感器体积也越大,所以, D 设置为 60 ~ 90 mm; 异径管段上下需要放置激励线圈,同时异径段前后需要有一定长度的过渡段来稳定流型,因此, L 设置为 60 ~ 120 mm。一共分析了 6 组 D × H 尺寸的传感器权函数分布随 L 的变化情况,如表 2 所示。由于电*截面内的权函数分布对感应电动势影响*大,因 此,利 用式( 10) 计算电*截面 xy 平面内的权函数整体均匀度 R。定义相同 D × H 条件下,权函数均匀度随 L 变化的波动率为 ML,如下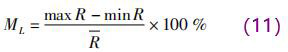
计算多组相同 D × H、不同 L 时 xy 平面的权函数整体均匀度 R 及波动率 ML,如表 1 所示。
通过表 1 分析可知,随着 L 的变化,权函数波动率ML≤ ±2. 5 % ,所以 xy 平面内的权函数整体均匀度变化较小,即长度 L 对电*截面内的权函数分布影响很小。
2) 宽度和高度的影响
通过上述分析可知,L 对传感器内的权函数分布影响很小,因此固定设置 L 为 80 mm。然后分析异径段 D,H 同时变化时的权函数分布情况。由上节可知,矩形异径截面的 D 设置为 60 ~ 90 mm,H 设置为 30 ~ 50 mm。为了便于分析三维权函数与 D,H 的变化关系,设置 H 与 D 变化步长都是 10 mm,因此,H 变化范围为 30 ~ 60 mm,即 D = { 60,70, 80,90 mm} ,H = { 30,40,50,60 mm} ,一共 16 组异径dn150供水计量表传感器结构。
分别对上述结构进行有限元分析,根据式( 10) 计算 xy平面内权函数整体均匀度 R,根据式( 11) 计算权函数随 H变化的波动率 MH,随 D 变化的波动率 MD,结果如表 2 所 示。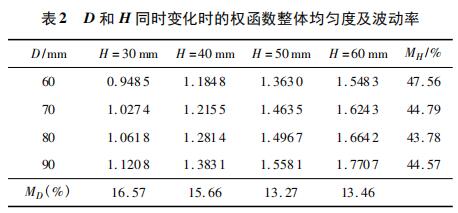
根据表 1 和表 2 权函数均匀度的波动率数值可以看出,MH > MD > ML,所以,矩形段 L,D,H 对于权函数均匀度的影响程度是依次增强的,高度 H 对权函数均匀度影响*大,宽度 D 影响稍小,长度 L 影响很小。且 D 和 H 越小,权函数整体均匀度 R 越小,权函数分布越均匀。
为了更加全面地比较权函数在三维空间的分布情况,从上述结构中选取 D × H = { 90 × 30,60 × 30,60 × 60} 三组典型结构,分析其权函数在 xy,xz,yz 三个平面内的分布情况。为了便于对比,统一规定三个平面内等势线的分布步长和数值范围: 1) xy,xz 平面内的权函数等势线大小以0. 25为步长,从 0 增加到 30; 2) 由于 yz 平面的权函数小于1,规定 yz 平面内的权函数等势线大小以 0. 05 为步长,从 0增加到 1。具体如图 3 ~ 图 5 所示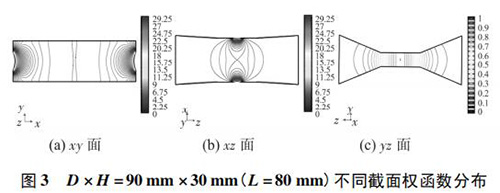
通过对图 3 ~ 图 5 分析得出以下结论: 1) 图 3( a) 、图 4( a) 的 xy 面权函数分布表明,D = 90 mm时中心区域的权函数等势线间距较大,即权函数变化梯度较小,且中心区域的权函数等势线逐渐变为直线,因此中心区域的权函数分布更均匀; 但 D = 90 mm 时,电*附近的权函数等势线较密,且等势线颜色较深,权函数*大值较大,变化梯度较大,所以,电*附近的权函数分布均匀性较差。因为难以直接衡量 D 改变时,xy 面权函数分布的均匀性。所以,需要利用权函数整体均匀度 R 定量确定 xy 平面内权函数分布的均匀性。结果表明,随着宽度 D 的减小,权函数分布越来越均匀。
2) 图 4( a) 、图 5( a) 的 xy 面权函数分布表明,H = 30 mm时中心区域的权函数等势线间距较大,且中心区域的权函数等势线逐渐变为直线; 电*附近的权函数等势线比较稀疏,且等势线颜色较浅,权函数*大值较小,变化梯度小,因 此,H = 30 mm 时 xy 面的权函数分布更加均匀。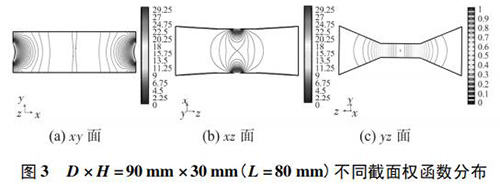
3) 图 3( b) ~ 5( b) 的 xz 面权函数分布表明,三组异径结构的权函数分布情况类似,没有明显的区别,即 D 和 H的变化对 xz 面的权函数分布影响较小。
4) 图 3( c) 、图 4( c) 的 yz 面权函数分布表明,D = 90 mm时的权函数等势线间距略大于 D = 60 mm 时的权函数等势线间距,权函数变化梯度较小,且中心区域的权函数等势线逐渐变为直线,因此 D = 90 mm 的权函数分布更均匀一些,但是两者区别很小,即宽度改变对 yz 面权函数分布影响很小。图 4( c) 、图 5( c) 的 yz 面权函数分布表明,H = 30 mm时的权函数等势线间距较大,且中心区域的权函数等势线逐渐变为直线,因此 H = 30 mm 的权函数分布更加均匀;
5) 图 3( a) ~ 5( a) 和图 3( b) ~ 5( b) 权函数分布结果表明,越靠近电*,等势线颜色越深,即权函数值越大,且越靠近电*,权函数等势线越密集,即权函数变化梯度越大。
综上所述,异径电磁水表异径段长度 L 对权函数分布的均匀性影响很小,随着长度 L 的改变,权函数分布基本没有变化; 异径段高度 H 对权函数分布的均匀性影响*大,宽度 D 影响稍小,高度和宽度越小,权函数分布越均匀,即异径dn150供水计量表传感器的测量精确度受非理想流场的影响越小。
3 结 论
1) 圆形、正方形、八边形和矩形等 4 种异径dn150供水计量表传感器的权函数分析结果表明,矩形异径截面传感器的权函数分布*均匀。
2) 电*附近区域,权函数值较大,且权函数变化梯度较大,随着远离电*,权函数值越来越小,且权函数变化梯度越来越小。
3) 矩形段高度 H 对权函数分布的均匀性影响*大,随 着 H 的减小,权函数分布越来越均匀,且 y 轴权函数的分布逐渐趋近于常数 1。矩形段宽度 D 对权函数分布的均匀性影响稍小,随着 D 的减小,权函数分布越来越均匀。矩形段长度 L 对传感器内的权函数分布影响很小,随着 L 的改变,权函数分布没有明显变化。



