1、引言
目前自来水流量的测量,倾向于使用非接触式的电子检测仪表。非接触式流量计大多采用超声技术。目前国内很多厂家推出了超声流量计,它们大多应用了微电脑处理技术,实现了测试的智能化。在国外,日本、德国、瑞士几家公司产品,其性能和原理大致相同。
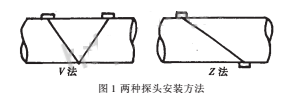
目前的流量计的基本测量原理和方法有以下三种:①时间差法,②相位差法,③频率差法。现在国内外的大多数非接触式超声流量计使用的都是频差法。例如富士株士会社生产的FLB-1型超声流量计使用的就是这种方法。它提供了可供选择的两种探头安装方法。如图1所示。其中V法适用于小管径的管道,而Z法则适用于2000mm或更大管径的管道。另外,当无法提供合适的安装间距时,宜于采用Z法,因为Z法仅需V法间距的一半,同时,在流体速度很高时,也应选择Z法。当管内壁的污垢很厚时,也不适用反射式的V法而选用Z法。但不论采用哪种方法,都很难排除随机的噪声干扰,造成较大的误差。因此,我们设计了一种新型的相关式超声流量计。
2、测量原理分析
相关检测技术在国内外文献中研究得很多,但在自来水流量测量中付诸实现仍是难的课题,本文所采用的相关检测方法如图2所示。在管道上装有两组传感器,上游传感器和下游传感器,两组传感器之间距离L。相关检测的实质是测出流体通过线性系统时,走过L长的距离所需的时间T。
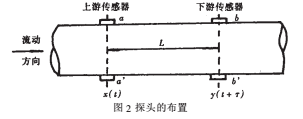
设上游传感器测得的信号是x(t),下游传感器测得的信号是y(t),对这两个信号进行互相关计算:
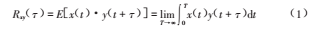
将系统的输入信号x(t)和输出信号y(t)**间的变化的记录分别看作是随机过程{xt(t)和yt(t)}的一个样本函数。由于系统是线性的,且不考虑噪声干扰的情况下,可以认为{xt(t)}和{yt(t+T)}是完全相似的,只是后者在时间上滞后T。事实上,由于附加噪声的干扰,二者的波形不可能完全相似。为了描述二者的畸变程度,引入差值函数e(t)。
e(t)=x(t)-Ay(t+T) (2)
其中,A是某一常数。显然,如果存在一个常数a使e(t)=0,则有:
x(t)=ay(t+T) (3)
如上所述,由于噪声的存在,常数a是找不到的。为了判断x(t)与y(t+T)波形相似程度,可采用随机函数方差的概念:
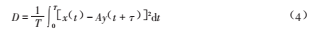
作为衡量x(t)和y(t+T)之间波形差异的一个尺度。按*小均方差为判据,D越小,则y(t+T)的波形与x(t)的波形相似程度越高。令dD/dA=0,可以解出D为*小值的A为

将式(5)代入式(4),化简后可得:
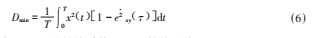
式中,exy(T)是相关系数lxy(T)的估计值,且


由于系统是线性的,系统的输出信号和输入信号**间的变化规律相同,只是它们在时间上相差一个T=To值,此值即为信号在该系统内的传递时间。在作相关运算时,互相关函数的Rxy(T)值将随x(t)与y(t+T)之间的相对延时值T的不同而变化。只有T的取值正好等于信号x(t)在系统中的传递时间To时,y(t+T)与x(t)二者的波形*为相似。此时,在互相关图上Rxy(T)也将出现峰值,如图3所示。
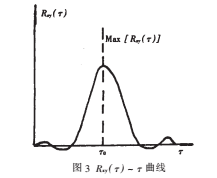

因此,根据Rxy(T)值的位置,可以确定信号x(t)在系统中传递时间To。
3、测试系统的软硬件设计
根据上述测量系统的数学模型,测试系统的硬件包括超声发射电路、传感器、超声接收电路、配用电路以及单片机和显示电路等部分组成,如图4所示。
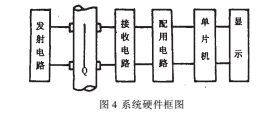
在本系统中,*为主要的是根据测量方法的数学模型,通过软件在单片机计算出To。因为L是固定的常数,To计算出来之后,即可根据
v=L/To (8)
计算出自来水的流速,进一步根据管径的大小计算出流量值。







